如果在一棵原本是平衡的avl树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,avl树的旋转分为四种。
1. 新节点插入较高左子树的左侧---左左:右单旋
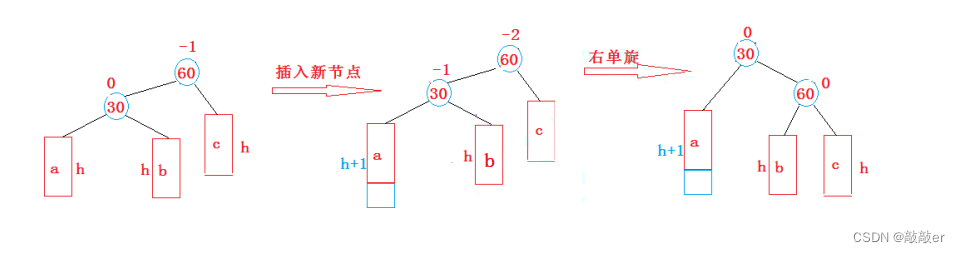
a/b/c分别是高度为h的avl子树
上图在插入前,avl树是平衡的,新节点插入到30的左子树(注意:此处不是左孩子)中,30左子树增加了一层,导致以60为根的二叉树不平衡,要让60平衡,只能将60左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点的平衡因子即可。在旋转过程中,有以下几种情况需要考虑:
1. 30节点的右孩子可能存在,也可能不存在
2. 60可能是根节点,也可能是子树
如果是根节点,旋转完成后,要更新根节点
如果是子树,可能是某个节点的左子树,也可能是右子树
代码
//右单旋
void rotater(node* parent)
{
node* subl = parent->_left;
node* sublr = subl->_right;
parent->_left = sublr;
if (sublr)
{
subl->_right = parent;
}
subl->_right = parent;
node* ppnode = parent->_parent;
parent->_parent = subl;
if (parent == _root)
{
_root = subl;
subl->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subl;
}
else
{
ppnode->_right = subl;
}
subl->_parent = ppnode;
}
parent->_bf = 0;
subl->_bf = 0;
}
2. 新节点插入较高右子树的右侧---右右:左单旋
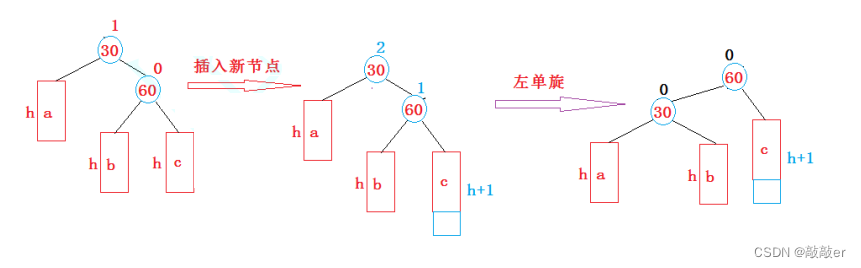
左单旋与右单旋的操作类似,只有左右节点的区别
代码
//左单旋
void rotatel(node* parent)
{
node* subr = parent->_right;
node* subrl = subr->_left;
parent->_right = subrl;
if (subrl)
{
subr->_left = parent;
}
subr->_left = parent;
node* ppnode = parent->_parent;
parent->_parent = subr;
if (parent == _root)
{
_root = subr;
subr->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = subr;
}
else
{
ppnode->_right = subr;
}
subr->_parent = ppnode;
}
parent->_bf = 0;
subr->_bf = 0;
}
3. 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
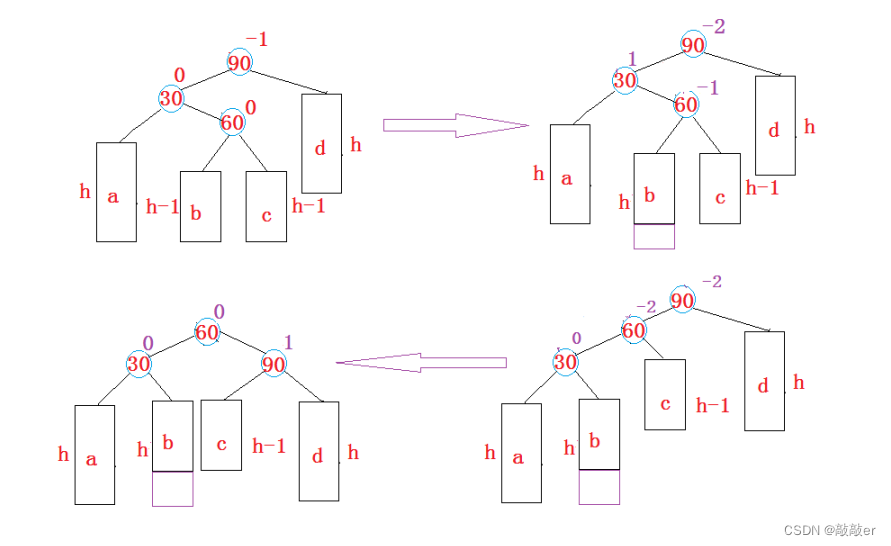
参考30和60的相对位置,将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
代码
//左右单旋
void rotatelr(node* parent)
{
node* subl = parent->_left;
node* sublr = subl->_right;
int bf = sublr->_bf;
rotatel(parent->_left);
rotater(parent);
if (bf == 1)
{
parent->_bf = 0;
subl->_bf = 0;
sublr->_bf = 1;
}
else if (bf == -1)
{
parent->_bf = 0;
subl->_bf = -1;
sublr->_bf = 0;
}
else if(bf==0)
{
parent->_bf = 0;
subl->_bf = 0;
sublr->_bf = 0;
}
else
{
assert(false);
}
}
4. 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
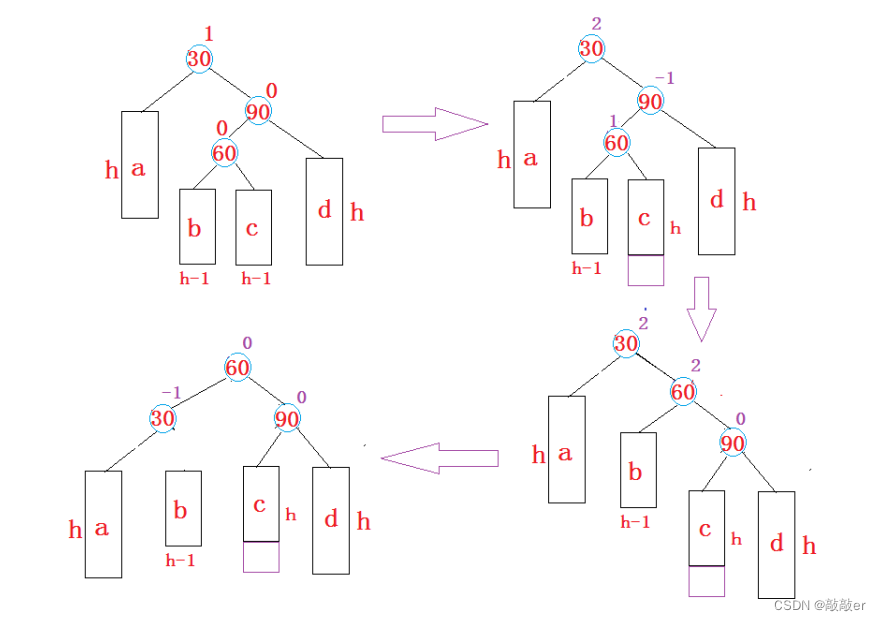
代码
//右左单旋
void rotaterl(node* parent)
{
node* subr = parent->_right;
node* subrl = subr->_left;
int bf = subrl->_bf;
rotater(parent->_right);
rotatel(parent);
if (bf == 1)
{
parent->_bf = 0;
subr->_bf = 0;
subrl->_bf = 1;
}
else if (bf == -1)
{
parent->_bf = 0;
subr->_bf = -1;
subrl->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subr->_bf = 0;
subrl->_bf = 0;
}
else
{
assert(false);
}
}
总结:
假如以pparent为根的子树不平衡,即pparent的平衡因子为2或者-2,分以下情况考虑:
1. pparent的平衡因子为2,说明pparent的右子树高,设pparent的右子树的根为psubr。
当psubr的平衡因子为1时,执行左单旋。
当psubr的平衡因子为-1时,执行右左双旋。
2. pparent的平衡因子为-2,说明pparent的左子树高,设pparent的左子树的根为psubl。
当psubl的平衡因子为-1是,执行右单旋。
当psubl的平衡因子为1时,执行左右双旋。
旋转完成后,原pparent为根的子树个高度降低,已经平衡,不需要再向上更新。

